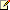 Important: Important: |
|---|
| This is retired content. This content is outdated and is no longer being maintained. It is provided as a courtesy for individuals who are still using these technologies. This content may contain URLs that were valid when originally published, but now link to sites or pages that no longer exist. |
The following table shows the functions applications can use to compute secure digests of data and to create and verify digital signatures.
| Function | Description |
|---|---|
|
Creates an empty hash object. |
|
|
Destroys a hash object. |
|
|
Retrieves a hash object parameter. |
|
|
Hashes a block of data, adding it to the specified hash object. |
|
|
Hashes a session key, adding it to the specified hash object. |
|
|
Sets a hash object parameter. |
|
|
Signs the specified hash object. |
|
|
Verifies a digital signature, given a handle to the hash object that was signed. |
To create a digital signature from a message, create a hash value, also known as a message digest, from the message. Then, use the signer's private key to sign the hash value. The following illustration shows the process for creating a digital signature.
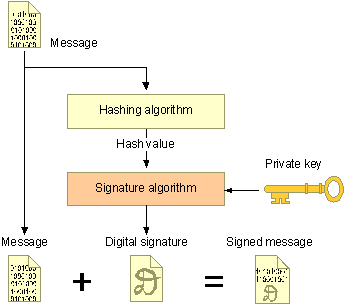
To verify a digital signature, both the message and the signature are required. First, a hash value must be created from the message in the same way as it was done when the signature was created. This hash value is then verified against the signature, using the public key of the signer. If the hash value and the signature match, you can be confident that the message is the one originally signed and that it has not been tampered with. The following illustration shows the process of verifying a digital signature.
A hash value consists of a small amount of binary data, typically 160 bits. It is produced using a hashing algorithm.
All hash values share the following properties, regardless of the algorithm used:
- A hash value is of a fixed length, regardless of the size of
the message.
- Every pair of nonidentical messages translates into a different
hash value, even if the two messages differ only by a single bit.
Using today's technology, it is not feasible to discover a pair of
messages that translate to the same hash value without breaking the
hashing algorithm.
- All hashing algorithms are fully deterministic. That is, each
time a particular message is hashed using the same algorithm, the
same hash value is produced.
- All hashing algorithms are one-way. Given a hash value, it is
not possible to recover the original message. In fact, none of the
properties of the original message can be determined with the hash
value alone.








 See Also
See Also